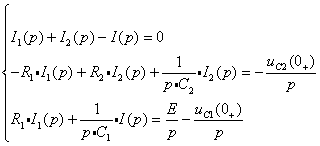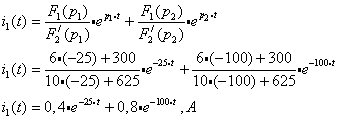Расчет переходных процессов в электрических цепях второго порядка операторным методом
Пример расчета
В соответствии с вариантом, заданным двумя последними цифрами шифра, указанного в зачетной книжке студента, выписать из таблиц 1 и 2 условия задания и выполнить следующее:
1. Начертить схему электрической цепи с обозначением узлов и элементов ветвей.
2. Рассчитать переходный процесс классическим методом, т.е. определить зависимости от времени мгновенных значений всех токов схемы и напряжения на всех ее пассивных элементах.
3. Рассчитать переходный процесс операторным методом, результаты сравнить с классическим.
4. Построить графики зависимостей от времени всех токов и напряжений на реактивных элементах.
Решение:
Классический метод см. тут

Дано:
E=120В, R1=100 Ом, R2=100 Ом,
C1=200 мкФ, C2=100 мкФ
Ii-?
II Операторный метод
1) Изобразим операторную схему замещения цепи для режима после коммутации:

Рисунок 3 –Схема замещения цепи
2) Запишем для нее систему уравнений по законам Кирхгофа в операторной форме:
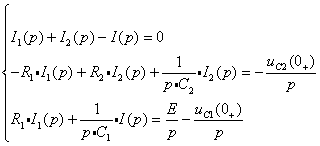
Решая ее относительно I1(p), после серии подстановок получаем следующие решение:
Примечание:
На самом деле все находится гораздо проще с помощью функции Find в Mathcad
Подставив числовые значения, получим:

3) По полученному изображению I1(p) найдем оригинал функции i1(t).
Примечание:
Нахождение оригинала функции - обратное преобразование Лапласа - легко осуществить с помощью Mathcad и функции invlaplace
Применим теорему разложения:

Найдем корни уравнения

По теореме разложения:
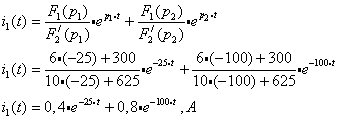
По закону Кирхгофа:


Полученные значения совпали с результатами, найденными с помощью классического метода.
Остальные величины определяются по законам Кирхгофа и Ома аналогично классическому методу.
III Построение графиков зависимостей от времени всех токов и напряжений на реактивных элементах.
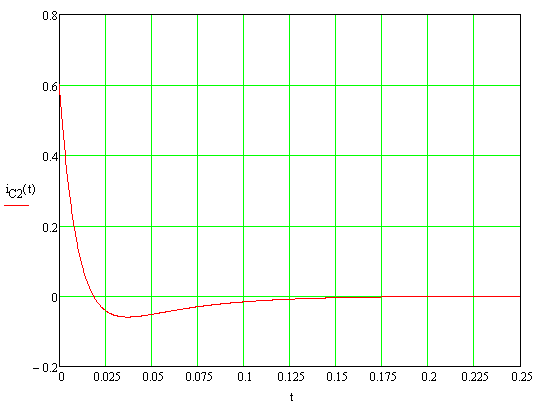
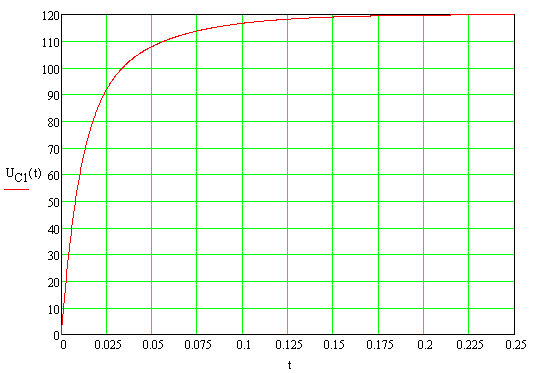
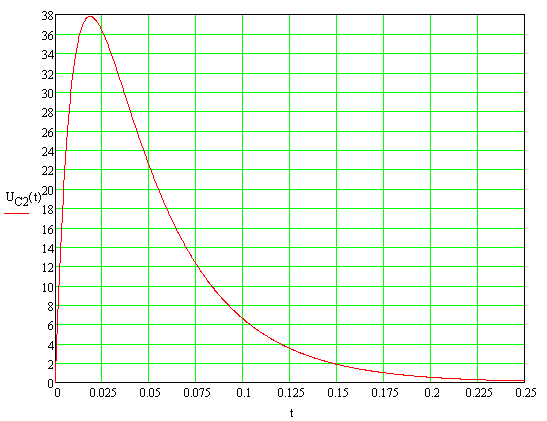
Для конденсаторов С1 и С2 построим зависимости тока и напряжения от времени (рисунок 4-7):
Рисунок 4 - График зависимости 
Рисунок 5 - График зависимости 
Рисунок 6 - График зависимости 
Рисунок 7 - График зависимости 
Эта же схема с применением классического метода
Назад к условию задачи